Řazení odporů

S řazením odporů se v elektrotechnice setkáváme velice často. Zde si to ukážeme na rezistorech, ale platí to obecně pro jakékoliv součástky, která klade odpor.

Pro začátek pro pochopení, takto vypadá zapojení měření hodnoty odporu rezistoru pomocí ohmmetru:

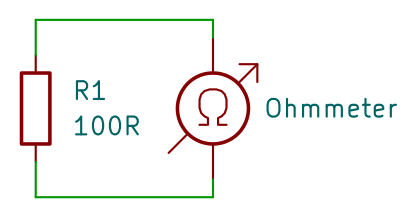
V tomto případě se na ohmmetru ukáže hodnota $100 \Omega$.

Proč rezistory řadíme?

Proč bychom vůbec rezistory nějak kombinovali, když existuje celá řada různých hodnot? Je pro to několik důvodů:

Různé řady rezistorů

Rezistory se vyrábí v různých řadách. Pokud bychom potřebovali nějakou přesnou hodnotu odporu (třeba $3 \Omega$), tak v řadě E12 (jedna z nejčastějších řad rezistorů) odpor přesně $3 \Omega$ nenajdeme. Můžeme si ale pomoct tak, že spojíme sériově 3x $1 \Omega$ odpory.

Výkonové použití

Rezistory mají maximální výkon, který zvládnou. Pokud se překročí, je možné, že rezistor shoří. Pokud ale zapojíme více (ideálně stejných) rezistorů paralelně, proud jimi se rozdělí a na každém bude menší výkon. Samozřejmě paralelním zapojením se změní i celková hodnota odporu, takže je potřeba s tím umět počítat.

Celkový přehled

Znalost různých zapojení rezistorů a dalších součástek patří k základním znalostem elektroniky. Bez schopnosti vypočítat sériové a paralelní spojení rezistorů se v elektronice nelze jednoduše orientovat.

Sériové zapojení

Sériové zapojení znamená to, že jsou součástky zapojeny "za sebou".

Analogie se silnicí

Rezistory si můžeme v tuto chvíli představit jako silnici. Stejně jako na silnici jezdí auta, tak zde prochází elektrický proud. Asi znáte situaci, kdy jedete v autě zúženou silnicí a musíte jet pomalu. Když zapojíme rezistory sériově, je to jako jet po takové silnici delší trasu. Elektrický proud je "zpomalován" každým rezistorem v sérii, což způsobuje snížení proudu.

Pokud máme sériové zapojení rezistorů, hodnota rezistorů se sčítá: $R = R_1 + R_2 + ...$

Výpočet:

$R = R_1 + R_2 = 100 + 200 = 300 \Omega$

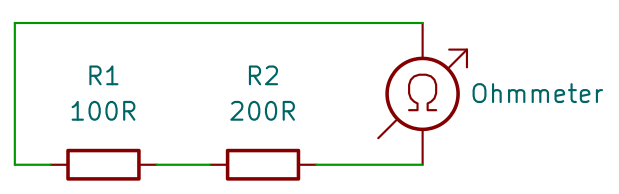
Paralelní zapojení

Paralelní zapojení znamená to, že jsou součástky zapojeny "vedle sebe".

Analogie se silnicí

Paralelní zapojení lze naopak přirovnat k víceproudové dálnici. Na dálnici se vedle sebe vejde více aut, proto jich může projet více. Stejné to je s elektrickým proudem. U paralerního zapojení se rozdělí do rezistorů a může proudu protéct více.

Hodnota odporu v paralelním zapojení je prevrácená hodnota součtu prevrácených hodnot každeho z odporů.

Základní vzorec:

$\dfrac{1}{R} = \dfrac{1}{R_1} + \dfrac{1}{R_2} + \dfrac{1}{R_3} + ...$

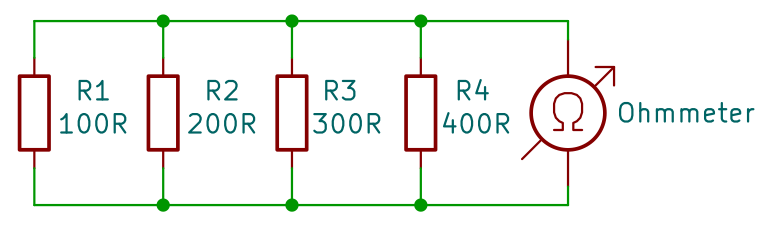
Tento vzorec můžeme upravit na tento tvar:

$R = \dfrac{1}{\dfrac{1}{R_1} + \dfrac{1}{R_2} + \dfrac{1}{R_3} + ...}$

Výpočet na kalkulačce

Většinu složitějších výpočtů nebudeme počítat "z hlavy". Zde je návod, jak zadávat zlomky na kalkulačce.

Výsledný odpor tohoto zapojení se počítá takto:

$R = \dfrac{1}{\dfrac{1}{R_1} + \dfrac{1}{R_2} + \dfrac{1}{R_3} + \dfrac{1}{R_4}} = \dfrac{1}{\dfrac{1}{100} + \dfrac{1}{200} + \dfrac{1}{300} + \dfrac{1}{400}} = \dfrac{1}{\dfrac{1}{48}} = 48 \Omega$

Výpočet pro 2 rezistory

Pro 2 rezistory můžeme použít jiný výpočet:

Výpočet:

$R = \dfrac{R_1 \cdot R_2}{R_1 + R_2} = \dfrac{200 \cdot 600}{200 + 600} = \dfrac{120000}{800} = 150 \Omega$

Zjednodušení - 2 stejné rezistory

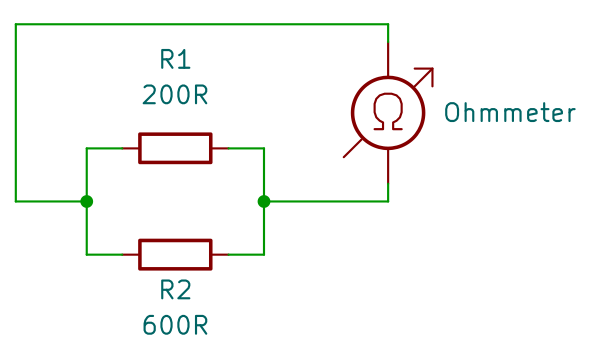
Pokud uvidíte někde paralelní zapojení 2 rezistorů, které mají stejný odpor, výsledná hodnota bude polovina hodnoty jednoho rezistoru.

Výpočet:

$R = \dfrac{R_1}{2} = \dfrac{200}{2} = 100 \Omega$

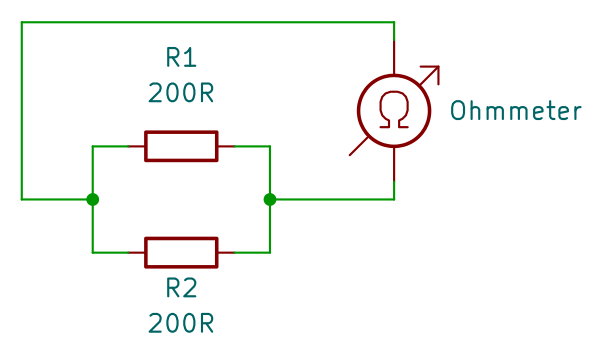
Když na to zkusíme použít postup z dřívějška, vyjde nám stejný výsledek:

$R = \dfrac{1}{\dfrac{1}{R_1} + \dfrac{1}{R_2}} = \dfrac{1}{\dfrac{1}{200} + \dfrac{1}{200}} = \dfrac{1}{\dfrac{1}{100}} = 100 \Omega$

Zjednodušení - více stejných rezistorů

Pokud uvidíte někde paralelní zapojení více rezistorů, které mají stejný odpor, výsledná hodnota bude $\dfrac{1}{{počet\ rezistorů}}$ hodnoty jednoho rezistoru.

Výpočet:

$R = \dfrac{R_1}{5} = \dfrac{500}{5} = 100 \Omega$

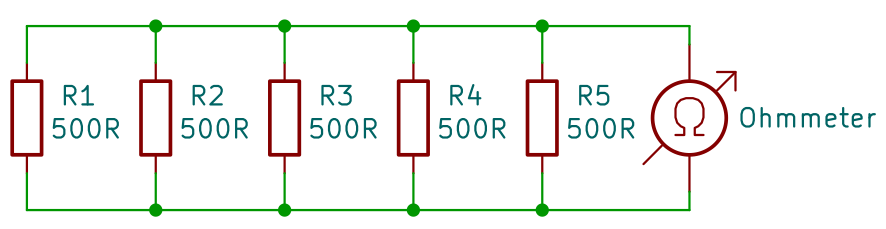
Když na to zkusíme použít postup z dřívějška, vyjde nám stejný výsledek:

$R = \dfrac{1}{\dfrac{1}{R_1} + \dfrac{1}{R_2} + \dfrac{1}{R_3} + \dfrac{1}{R_4} + \dfrac{1}{R_5}} = \dfrac{1}{\dfrac{1}{500} + \dfrac{1}{500} + \dfrac{1}{500} + \dfrac{1}{500} + \dfrac{1}{500}} = 100 \Omega$

Kombinované zapojení

V praxi se velmi často setkáváme s kombinací serio-paralelního zapojení. Tyto případy je nutné řešit postupným zjednodušováním. Více se dozvíte na stránce Kombinované zapojení.