Kombinované zapojení

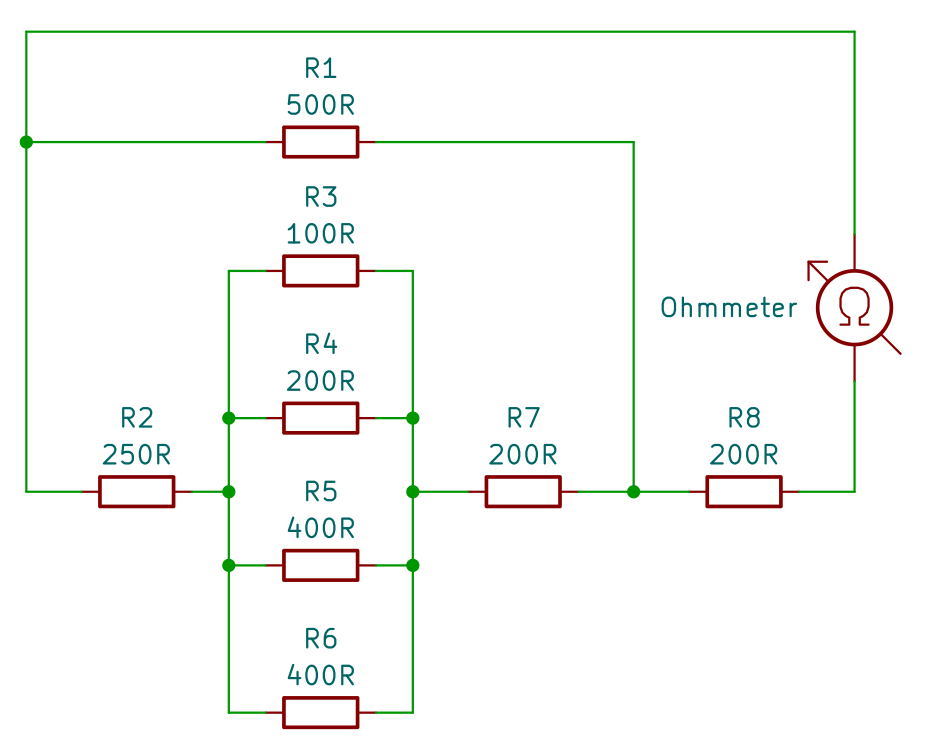Takto vypadá kombinované zapojení. Abychom ho vyřešili, řídíme se metodou rozděl a panuj.

Schéma si rozdělíme na několik částí. Začínáme vždy operací, u které známe všechny hodnoty. To znamená, že nemůžeme počítat sériové zapojení rezistoru $R_2$ a $R_3$, protože rezistor $R_3$ je zapojen paralelně s dalšími rezistory a my zatím neznáme výslednou hodnotu jejich odporu. Postupně počítáme hodnoty odporu jednotilvých spojení, dokud nemáme výslednou hodnotu.

Toto zapojení je už pokročilejší, použijeme znalosti z předchozích zapojení.

Výpočet

Začneme u rezistorů $R_3, R_4, R_5, R_6$ a jejich společný odpor označíme $R_{3456}$

$R_{3456} = \dfrac{1}{\dfrac{1}{R_3} + \dfrac{1}{R_4} + \dfrac{1}{R_5} + \dfrac{1}{R_6}} = \dfrac{1}{\dfrac{1}{100} + \dfrac{1}{200} + \dfrac{1}{400} + \dfrac{1}{400}} = \dfrac{1}{\dfrac{1}{50}} = 50 \Omega$

krok 2

Pokračujeme sériovým spojením $R_2, R_{3456}$ a $R_7$, které označíme $R_{234567}$.

$R_{234567} = R_2 + R_{3456} + R_7 = 250 + 50 + 200 = 500 \Omega$

krok 3

$R_{234567}$ je paralelně zapojen s $R_1$, takže provedeme výpočet:

$R_{1234567} = \dfrac{R_1 \cdot R_{234567}}{R_1 + R_{234567}} = \dfrac{500 \cdot 500}{500 + 500} = \dfrac{250000}{1000} = 250 \Omega$

krok 4

Nakonec stačí spočítat sériové spojení $R_{1234567}$ a $R_8$:

$R = R_{1234567} + R_8 = 250 + 200 = 450 \Omega$

Kombinované zapojení na procvičení

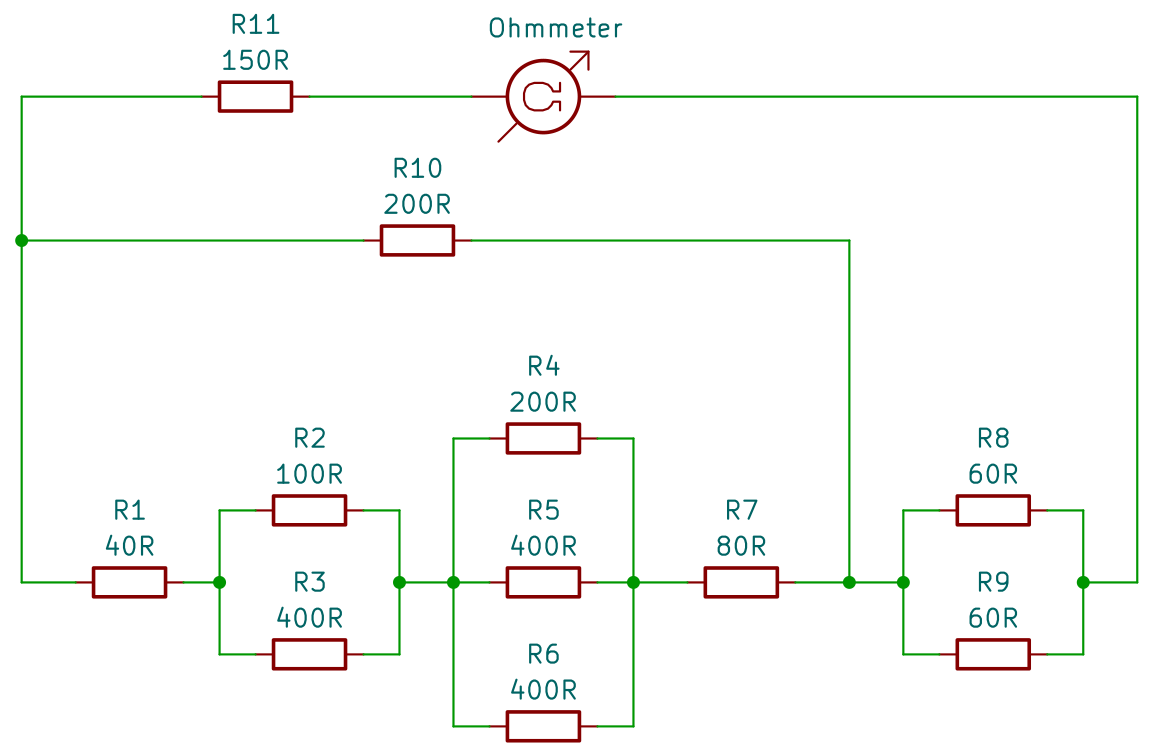
Zde je příklad na spočítání celkového odporu.

Výsledek

$300 \Omega$